Table of contents
Cache simulator
Number of sets:
Number of ways:
Block size (words):
Insert element (address):
Introduction
Over the years, a performance gap has formed between the processor and the memory unit. As shown in the figure below, processor performance has been increasing much faster than memory performance. Consequently, the processor has become much faster than the memory, forming a bottleneck for the performance of the computer in general.
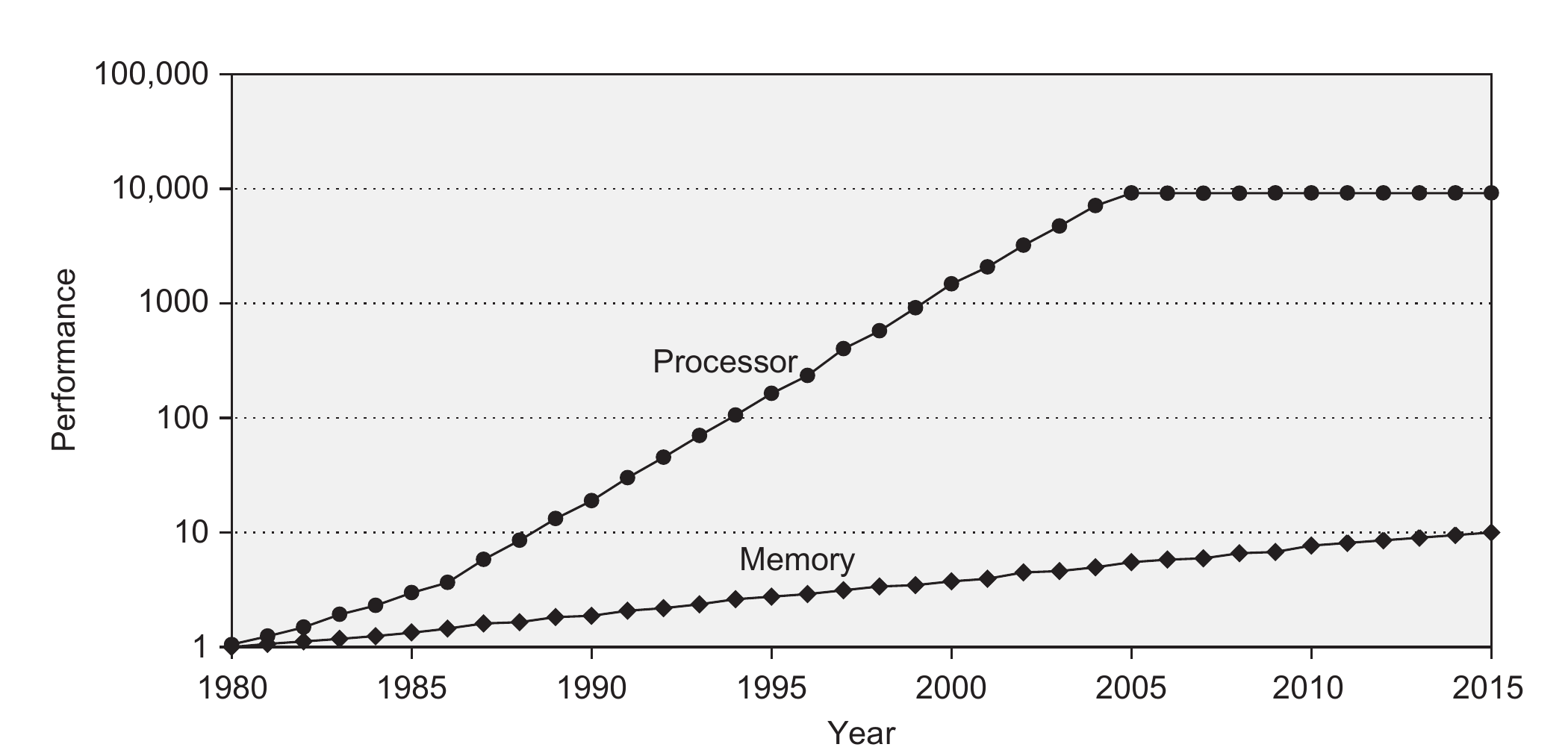
To solve this issue, caches were introduced. Cache memories are not as fast as registers, but can include more data, and are much faster than the main memory. However, they are also more expensive than the main memory and therefore a lot smaller. Most commercial CPUs typically offer a hierarchy of caches: Level 1 cache (L1) is the fastest but also the smallest cache, Level 2 cache (L2) is slower but larger, and the last level cache (L3 or LLC), which is the slowest but the biggest.
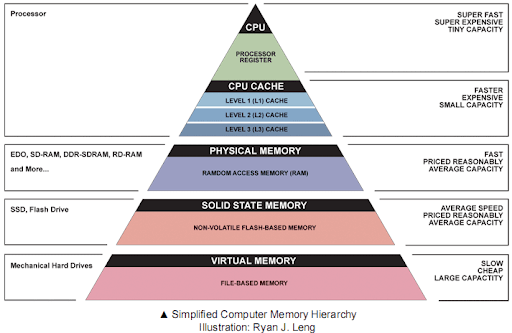
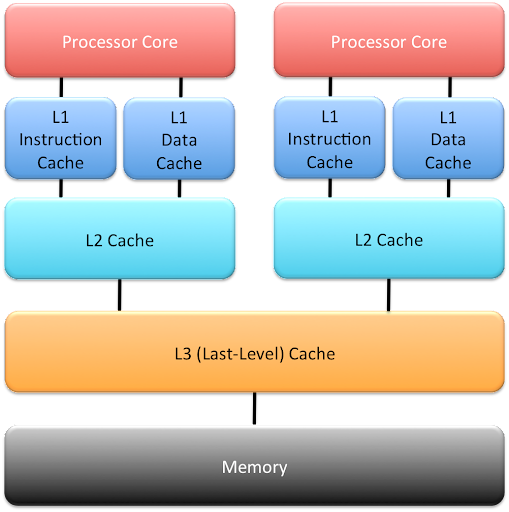
Caches can be local to a single processor core (this is typically for case for L1 and L2 caches), or shared across multiple cores. Finally, the L1 cache is usually split into an instruction cache (L1I), which contains program instructions, and a data cache (L1D), which contains program data.
Locality principle
Programs usually access a relatively small portion of the address space at a time.
In particular, when a program accesses a given memory location (a variable), it is likely to access that same location again in the near future. This is called temporal locality. Hence, a memory location that is accessed by a program can be cached to speed up future accesses!
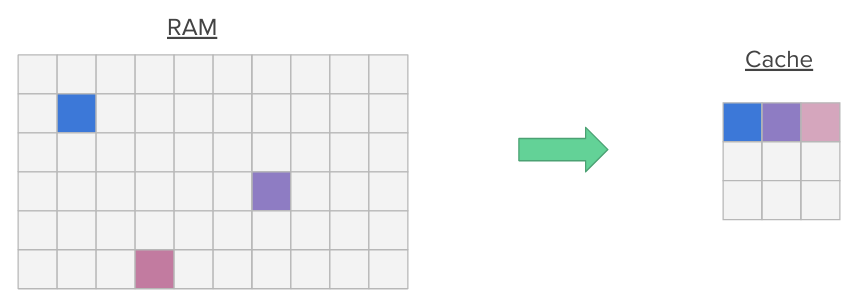
Additionally, when a program accesses a memory location, it is likely to access nearby memory locations in a near future (think for instance about nearby variables on the stack or nearby array members). This is called spatial locality. Hence, when a memory location is accessed, we transfer entire blocks (multiple contiguous words in memory) into the cache at once, pulling nearby data into the cache.
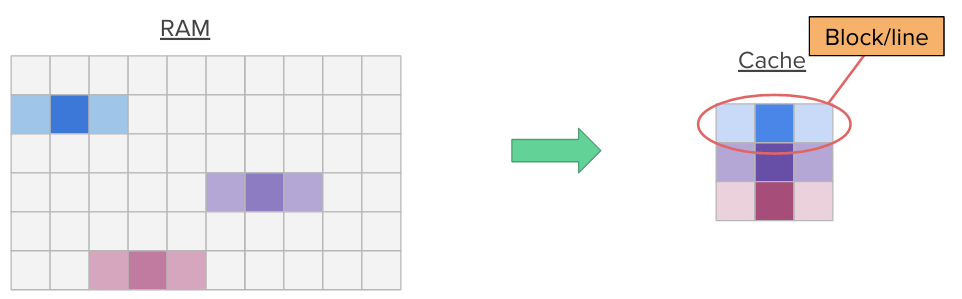
By exploiting these two locality principles, caches can cause a huge performance gain, even though they are small.
Terminology
Consider a program that accesses a memory address: lw t0, 0x10010000.
We say that we have a cache miss if the address 0x10010000 is not in the cache (for instance if it is the first time it is accessed by the program). In that case, the value is requested from the DRAM and the memory access is slow. The value is then placed in the cache for later use (following the temporal locality principle).
We say that we have a cache hit if the address 0x10010000 is in the cache. In this case, the corresponding value is directly served from the cache and the memory access is fast.
We can express the performance of the caching algorithm with the hit rate, which is the number of cache hits divided by the total number of memory accesses. We can also talk about the miss rate, which is equal to (1 - hit rate), or (cache misses / total accesses).
Timing attacks
Caches introduce timing variations based on the memory accesses of a program. This means that an attacker can use timing to infer which memory addresses are accessed by a victim program! In particular, on shared architectures (for instance a remote server shared between multiple users), an attacker can monitor the state of the cache (by observing cache hits and misses) to infer which cache lines are accessed by a victim. If the memory addresses accessed by the victim depend on secret data, the attacker can ultimately infer information about this secret data, leading to critical security vulnerabilities.
Attacks that exploit the state of the cache as a way to leak secret data are called cache attacks. They are part of a more general class of attacks, called timing attacks, which exploit timing variations of a system to leak secret data.
We will see two different examples of cache attacks later in the session. But first, let’s illustrate basic timing attacks with some exercises.
Exercise 1: Mount a timing attack
First, download the archive code.zip, which contains the program for this exercise and the next one. The file passwd.c contains the code of a password checker. In this exercise, you have to infer the value of the password using a timing attack. (The password is given in secret.h, so for the sake of the exercise, please do not open this file!)
- Examine the source code in
passwd.c, then compile and run the program, and try to guess the correct password! - Explain why the execution timings being printed are not always exactly the same when repeatedly providing the exact same input. Why is it a good idea to print the median instead of the average?
- Can you identify a timing side-channel in the code? Keep in mind that you only control the
useranduser_lenarguments (by providing inputs to the program), whilesecretandsecret_lenremain fixed unknown values. Hint: Try to come up with a way to iteratively provide inputs and learn something useful from the associated timings. First infersecret_len, before finally inferring all the secret bytes. You can assume the secret PIN code uses only numeric digits (0-9).
$ gcc passwd.c -o passwd
$ ./passwd
Enter super secret password ('q' to exit): 32349
--> You entered: '32349'
_______________
< ACCESS DENIED >
---------------
\
\
\|/ ____ \|/
"@'/ .. \`@"
/_| \__/ |_\
\__U_/
time (med clock cycles): 68
Solution
In the program ( passwd.c ), we see that the printed execution time is the calculated median over 100,000 measurements:
for (j = 0; j < NUM_SAMPLES; j++)
{
tsc1 = rdtsc_begin();
allowed = check_pwd(pwd);
tsc2 = rdtsc_end();
diff[j] = tsc2 - tsc1;
}
// ...
qsort(diff, NUM_SAMPLES, sizeof(uint64_t), compare);
med = diff[NUM_SAMPLES/2];
Even with this measure, we might notice different time values for the same inputs. This happens because the timing of one execution depends on many factors. Modern processors include a wide range of microarchitectural optimizations, such as instruction and data caches, pipelining, branch prediction, dynamic frequency scaling, out-of-order execution, etc. The execution can also be delayed by external events, such as an interrupt that is handled by the operating system. Taking the median instead of the average reduces the effect of such outliers.
It’s time to guess the password. First, we can notice that the program exits immediately if we provide a password with an incorrect length.
if (user_len != secret_len)
return 0;
If we guess the length incorrectly, the program exits. If we guess it correctly, it continues to compare the individual characters in the password.
This means that based on the execution time, we can tell whether we guessed the length correctly: the program will take longer to execute in that case.
Enter super secret password ('q' to exit): 0
time (med clock cycles): 68
Enter super secret password ('q' to exit): 00
time (med clock cycles): 70
Enter super secret password ('q' to exit): 000
time (med clock cycles): 372
Now we know that the password consists of 3 characters.
Let us examine how the program compares the individual characters:
for (i = 0; i < user_len; i++)
{
if (user[i] != secret_pwd[i])
return 0;
}
The same principle applies here: the program quits at the first character that does not match. This means that the longer the execution takes, the more characters at the start of the password we managed to guess correctly.
This way, we can guess the characters one-by-one, starting from the start of the string. Assuming that the password is a pin made of N digits, this means that to guess the entire password, we need a total of N * 10 guesses. Compare this with 10^N guesses if we could not guess one-by-one, but would have to iterate over every possible combination!
Enter super secret password ('q' to exit): 200
time (med clock cycles): 372
Enter super secret password ('q' to exit): 300
time (med clock cycles): 372
Enter super secret password ('q' to exit): 400
time (med clock cycles): 372
Enter super secret password ('q' to exit): 500
time (med clock cycles): 782
Enter super secret password ('q' to exit): 510
time (med clock cycles): 784
Enter super secret password ('q' to exit): 520
time (med clock cycles): 1072
Enter super secret password ('q' to exit): 522
time (med clock cycles): 1070
Enter super secret password ('q' to exit): 523
time (med clock cycles): 1070
Enter super secret password ('q' to exit): 524
-\-> You entered: '524'
_______________
< ACCESS ALLOWED >
---------------
\
\
.--.
|o_o |
|:_/ |
// \ \
(| | )
/'\_ _/`\
\___)=(___/
time (med clock cycles): 1342
Basic cache attack: Flush+Reload
Cache attacks, just as the timing attack on the password checker illustrated above, exploit variations of execution time to infer secret data. By measuring the execution time of a memory access, an attacker can determine whether a memory access results in a cache hit or a cache miss. Using this information, the attacker can determine if a victim has accessed the same memory location!
Let us look at a basic cache attack, called Flush+Reload. Flush+Reload relies on an instruction, offered by some CPUs, to flush (remove data from) the cache. We illustrate Flush+Reload with a step-by-step example (notice that each item number corresponds to a slide in the slideshow below):
- Consider that an attacker and a victim share some memory so that a variable
ais accessible to both the attacker and the victim; -
Flush: the attacker flushes the address
&afrom the cache; -
Victim executes: The attacker lets the victim execute. If
secret == 1, the victim requests the address&a, which produces a cache miss; - The address
&ais then requested from DRAM and placed in the cache; -
Reload: The attacker tries to access again the address
&aand times the memory access. If the access is fast (cache hit) then the attacker can infer that the value has been accessed by the victim, and therefore thatsecret == 1; - Alternatively, the attacker can try to access the variable
b. Because the access is slow (cache miss), the attacker can infer that the value has not been accessed by the victim, and again conclude thatsecret == 1.
Flush+Reload is a very reliable and easy attack as it does not require knowledge of internal cache organization. However, it requires shared memory between an attacker and its victim (such that both have access to a and b) and hence is only applicable in a limited number of scenarios.
Exercise 2: Mount a Flush+Reload attack
The flush_and_reload.c of the code.zip archive file contains the following function:
void secret_vote(char candidate)
{
if (candidate == 'a')
votes_a++;
else
votes_b++;
}
We want to detect which of the candidates the user voted for. To increase the vote count for candidate a or for candidate b, the program first has to load the corresponding current number of votes from memory (i.e. votes_a or votes_b). This is the access we will try to detect. Based on whether votes_a or votes_b has been accessed, we know which candidate got the vote.
Write down the three steps required to mount a successful Flush+Reload attack on this program.
Solution
Using the Flush+Reload technique, we (as the attacker) need to take the following steps:
- Flush
votes_afrom the cache; - Let the
secret_votefunction execute with a secret inputcandidate. This will load the value of eithervotes_aorvotes_bfrom memory, and place it in the cache; - After the execution is done, reload
votes_a. If the access time is low, this signals a cache hit. A cache hit in turn indicates that the victim process has accessedvotes_a, which means a vote for candidate A. On the other hand, if the access time is high, this means the value has not been cached, this is not the candidate the user voted for.
Of course, the above process could be executed with votes_b in place of votes_a. Since there are only two candidates, it suffices to check whether one of the two variables has been accessed.
Edit the main function in flush_and_reload.c to implement the missing flush and reload attacker phases. You can use the provided void flush(void *adrs) and int reload(void *adrs) functions. The latter returns the number of CPU cycles needed for the reload. If necessary, compensate for timing noise from modern processor optimizations by repeating the experiment (steps 1-3 above) a sufficient number of times and taking the median or average.
You can compile and run the program with:
$ gcc flush_and_reload.c -o fnr
$ ./fnr
Solution
In order to draw a conclusion in the above example, we need to have an idea about what a “low” and “high” access time is. To make our job easier, we can just measure the access time of both the votes_a and votes_b variables and see which one takes considerably less time: that one is the one the user voted for.
Using the provided functions, this is simply:
flush(&votes_a);
flush(&votes_b);
secret_vote('b');
time_a = reload(&votes_a);
time_b = reload(&votes_b);
Similarly to the previous example, we will compensate for variations in the timings by averaging the measurements over multiple executions. The final code is thus:
int SAMPLES = 1000;
unsigned long long time_a = 0, time_b = 0;
for (int i = 0; i < SAMPLES; ++i) {
flush(&votes_a);
flush(&votes_b);
secret_vote('b');
time_a += reload(&votes_a);
time_b += reload(&votes_b);
}
printf("A avg: %llu, B avg: %llu\n", time_a / SAMPLES, time_b / SAMPLES);
This will provide us with an output from which it is clear to see which candidate has been voted for:
$ gcc flush_and_reload.c -o fnr
$ ./fnr
A avg: 419, B avg: 120
Cache placement policies
The cache placement policy determines where a memory address should be placed in the cache.
Direct mapping
Let us start with the structure of the cache. In our examples, we consider byte-addressable memory, meaning that data is stored and accessed byte-per-byte (contrary to a word-addressable memory where data is stored word-per-word). The cache is a table that contains multiple rows, these are called the cache sets. A cache set can include one or more cache blocks (a block is sometimes also called a cache line, which can be slightly confusing in our representation, since a cache set is represented as a row [or line] in the cache table, which can contain multiple cache lines).
The simplest cache placement policy, called direct mapping, maps every memory address to a unique block in the cache.
Take for instance the cache model given below, where each cache set only contains a single block. Given a memory address, the index of the corresponding cache set is determined using the two least significant bits of the address (index = adress % 4). Because multiple addresses map to a single cache block, the cache also needs to keep track of a tag, corresponding to the most significant bits of the address. Therefore, given an address, the index determines where to look for the data in the cache and the tag indicates whether we have a cache hit or a cache miss.
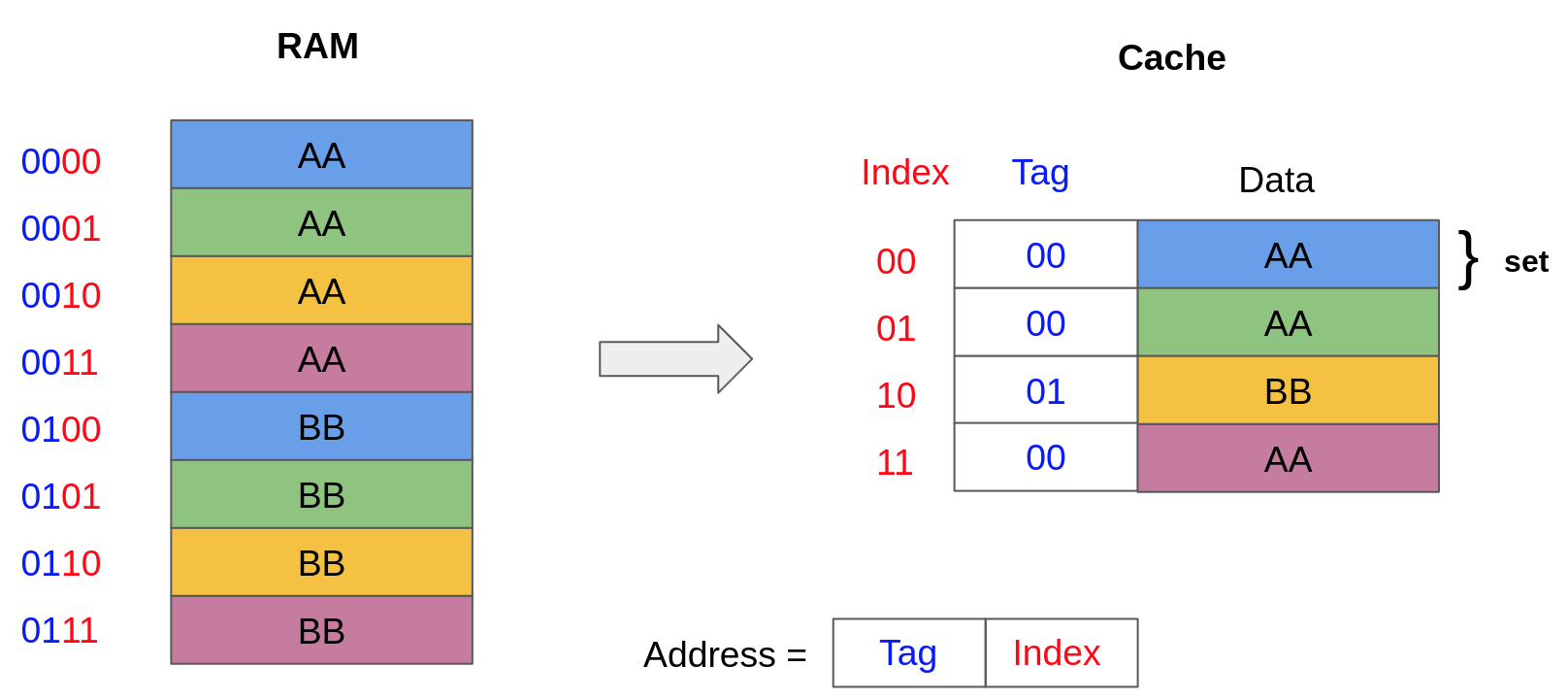
A memory address, composed of a tag t and an index i, is in the cache (cache hit) if the tag at index i in the cache matches t. For instance, accessing the address 0001 (i.e. tag=00, index=01) results in a cache hit because the tag in the cache at index 01 is 00. However, accessing the address 0010 (i.e. tag=00, index=10) results in a cache miss because the tag in the cache at index 10 is 01.
The data in one cache block typically contains more than one byte. This is to enable spatial locality: when the data from a certain address is loaded, the contents of the neighboring memory locations are also placed in the cache, in case they are also accessed in the future.
For instance, in the cache model given below, the size of a block is 4 bytes. The lower bits of the address correspond to the offset of the data in a cache block. For instance, the address 001000 corresponds to the value A0, while the address 001001 corresponds to the value A1.
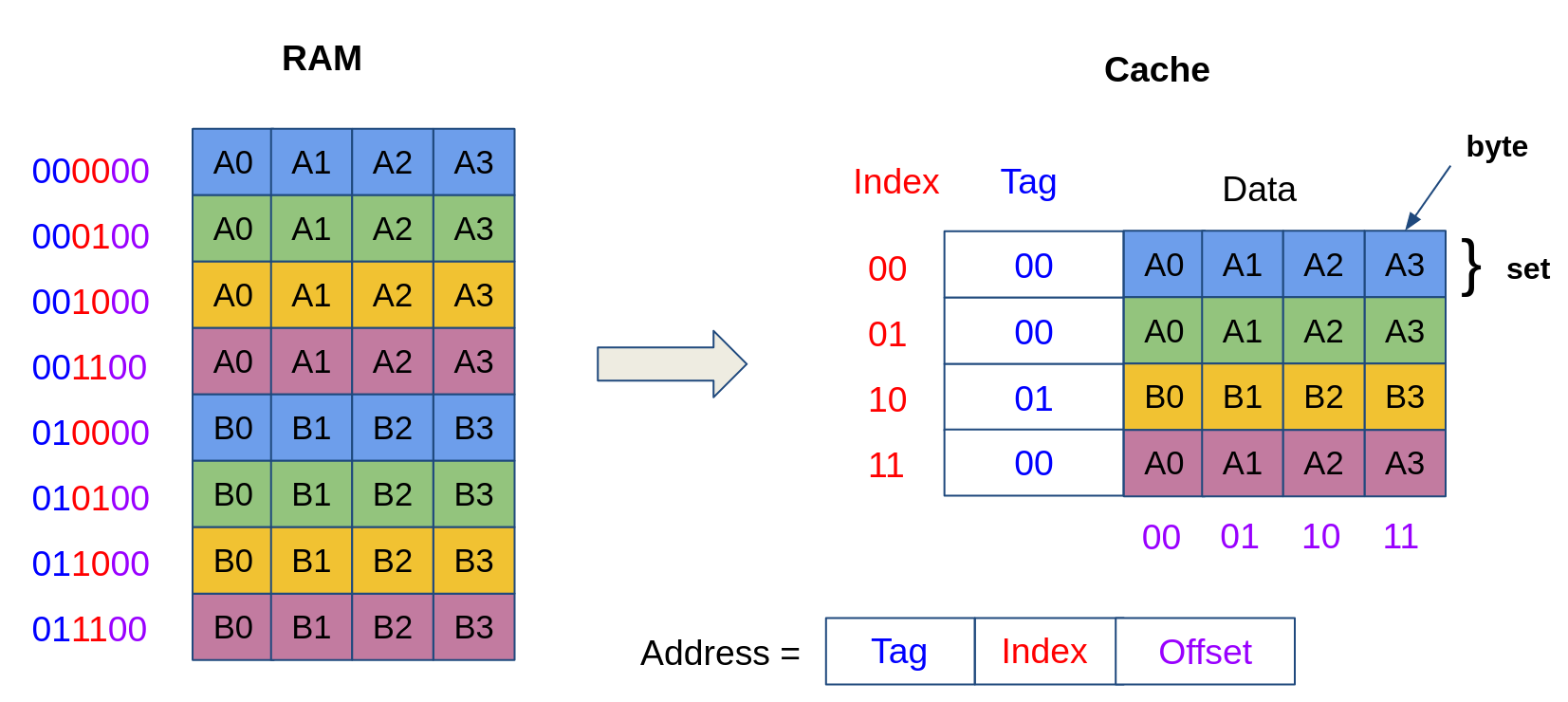
Summary.
A memory address (of size 32 bits) is composed of:
- an offset (the least significant bits of b) which determines the offset into one cache block;
- an index (the next k bits), which determines the cache set;
- a tag (the remaining 32-(k+b) most significant bits), which determines whether we have a cache miss or a cache hit. Additionally, the cache contains a Valid bit, which indicates whether a cache line is valid or not (e.g., in order to synchronize data across different caches).

Set-associativity
A limitation of direct-mapped caches is that there is only one block available in a set. Every time a new memory address is referenced that is mapped to the same set, the entire block is replaced, which causes a cache miss. Imagine for instance a program that frequently accesses addresses 000100 and 010100 in the above illustration. Because both addresses map to the same cache set (at index 01), accessing 010100 evicts 000100 from the cache (and vice versa). Hence, accessing both addresses in an alternating fashion results in a sequence of cache misses, which causes a performance loss.
To mitigate this problem, we can duplicate our cache structure into multiple ways, where a given address can be placed into any of the ways. We illustrate below a 2-way cache. Now, even though 000100 and 010100 map to the same cache set (at index 01), they can be placed in two different ways and can be in the cache at the same time!
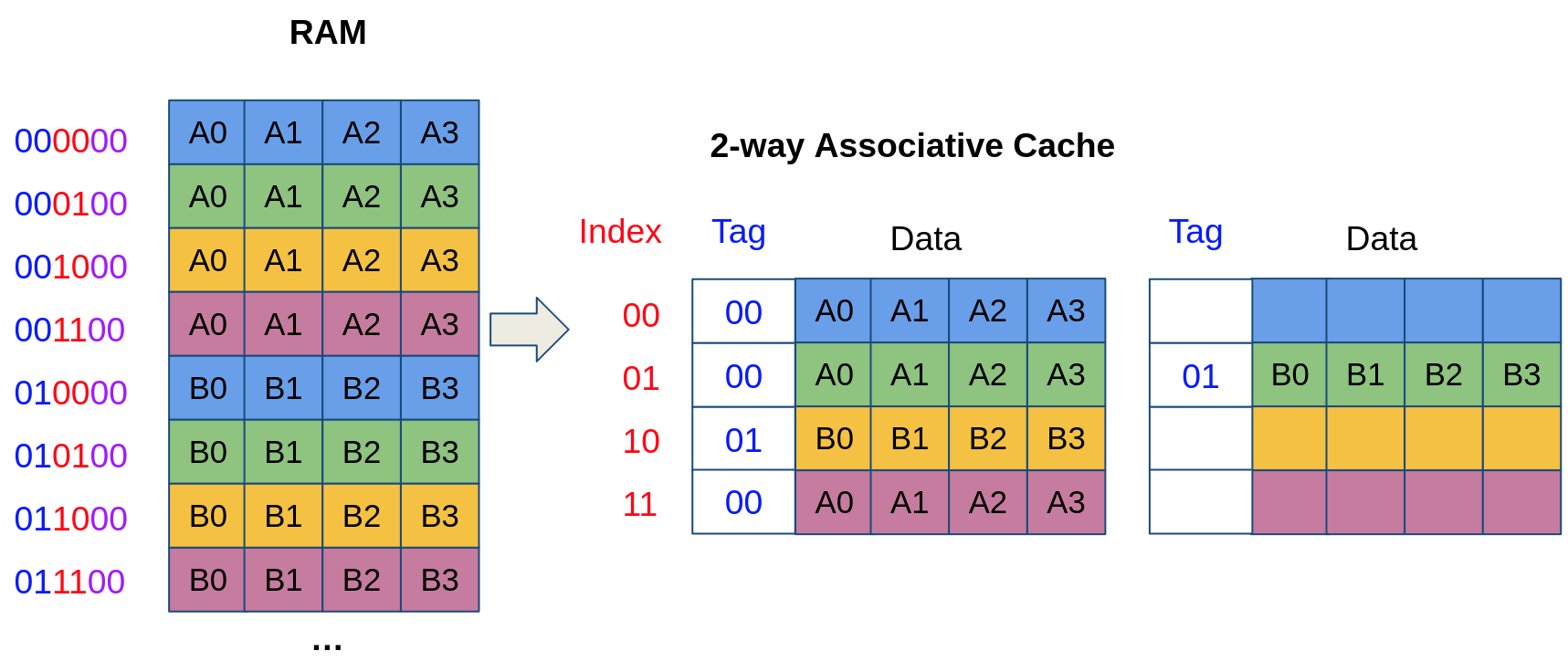
Finally, a fully associative cache is made up of a single cache set containing multiple ways. Hence, a memory address can occupy any of the ways and is solely identified with its tag (no need for an index because there is only one set!). Fully-associative caches ensure full utilization of the cache: a block is never evicted if the cache is not full. When the cache is full, the evicted line is determined by a replacement policy (e.g., the least recently used block is replaced). However, searching for an address in a fully associative cache is expensive: it takes time (and power) to iterate through all cache blocks and find a matching tag.
Notice that a 1-way associative cache corresponds to a direct-mapped cache. Hence, an n-way set-associative cache provides an interesting tradeoff between a direct-mapped cache and a fully associative cache.
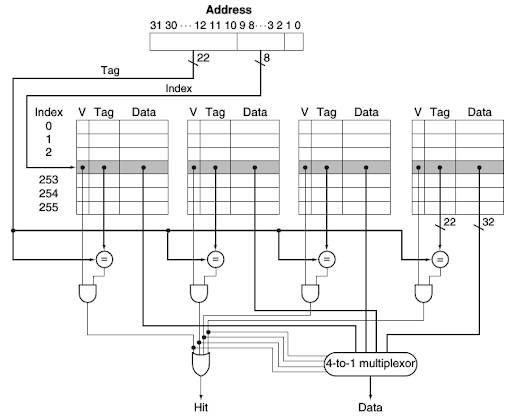
Exercise 3
Suppose a computer’s address size is k bits (using byte addressing), the cache data size (the total of the stored data, excluding the metadata such as tags) is S bytes, the block size is B bytes, and the cache is A-way set-associative. Assume that B is a power of two, so B=2^b. Figure out what the following quantities are in terms of S, B, A, b and k:
- the number of sets in the cache;
- the number of index bits in the address;
- the number of bits needed to implement the cache.
Solution
In this case, we have A number of ways.
Way 1 Way 2 Way A
+---+------------+------------+ +---+------------+------------+ ... +---+------------+------------+
| V | Tag | Data | | V | Tag | Data | ... | V | Tag | Data |
+---+------------+------------+ +---+------------+------------+ ... +---+------------+------------+
| | | .......... | | | | .......... | ... | | | .......... |
+---+------------+------------+ +---+------------+------------+ ... +---+------------+------------+
| | | | | | | | ... | | | |
+---+------------+------------+ +---+------------+------------+ ... +---+------------+------------+
| | | | | | | | ... | | | |
+---+------------+------------+ +---+------------+------------+ ... +---+------------+------------+
Another piece of information we are given is the cache data size, S bytes. This is the total size of all the data blocks, across all ways and sets. This already gives us enough information to calculate the number of sets. The total cache data size is S , this divided by the number of ways, A , gives us the data size of one way ( = S/A ). Dividing this with the block size, B , gives us the number of blocks in one way, which is the number of sets ( = S/(A*B) ).
We are told that the memory is byte-addressable (one memory address corresponds to one byte of data). One such address consists of k bits. In the context of the cache, this address is divided into three parts.
k 0
+-----+-------------+----------------+
| Tag | Set index | Index in block |
+-----+-------------+----------------+
log2(S/(A*B)) b
The least significant bits select the addressed byte from the data block. This data block contains 2^b bytes, which are addressable using exactly b bits (as the number x can be represented using log_2(x) bits).
The next bits select the cache set (referred to as the set index). The same principle applies here. As we know that there are S/(A*B) sets, these can be indexed using log_2(S/(A*B)) bits.
The remainder of the address is used as the tag in the cache. This part of the address makes sure that even if the lower bits of two addresses are equal, the value of one cannot be loaded from the cache when the other one is accessed (because the tag equality check is going to fail). The size of this tag is thus k - log_2(S/(A*B)) - b bits (the total length of the address minus the previous two fields).
We can now calculate the total size of the cache. There are a total number of S/B blocks (total data size / block size). Each block contains 8B data bits and contains the following metadata: 1 valid bit and the tag bits. All together, the cache size is:
= S/B * (8B + 1 + (k - log_2(S/(A*B)) - b))
Exercise 4
Consider a processor with a 32-bit addressing mode and a direct mapped cache, with 8-word block size and a total size of 1024 blocks. Calculate how many bits of the address are used to tag a block, to select the block, a word in the block, a byte in the word. The sum of these numbers must be 32! Calculate the total size needed to implement this cache.
Solution
We see that we have a total number of 1024 blocks. Because this is a direct mapped cache, we also know that the number of blocks equals the number of sets, as there are no additional ways in the cache. From this, we can already conclude that we need log_2(1024) = 10 index blocks to select the set.
We also know that one block contains 8 words. To index one of these words, we need log_2(8) = 3 bits. The 32-bit addressing mode means that one word is 32 bits, 4 bytes long. To select one byte from this word, we need thus log_2(4) = 2 more bits.
This completes the addressing, which means that the remainder of the memory address is used as the tag in the cache. This is 32 - 10 - 3 - 2 = 17 bits.
The total size of the cache is, using a similar calculation as before:
= 1024 * (8 * 32 + 1 + 17)
For each set, we have a block size of 8 * 32 bits, and we have one valid bit and 17 tag bits per line.
Exercise 5
Here is a series of address references given as word addresses: 2, 3, 11, 16, 21, 13, 64, 48, 19, 11, 3, 22, 4, 27, 11. Label each reference in the list as a hit or a miss and show the final content of the cache, assuming:
- direct-mapped cache with 16 1-word blocks that is initially empty;
- direct-mapped cache with 4-word block size and total size of 16 words;
- 2-way set-associative cache, 2-word block size. Total size of 16 words.
The following table shows an example format of a possible solution for a direct-mapped cache with 8 2-word blocks.
+---+----+----+
| S | W0 | W1 |
+---+----+----+
| 0 | 48 | 49 |
| 1 | 2 | 3 |
| 2 | 4 | 5 |
| 3 | 22 | 23 |
| 4 | -- | -- |
| 5 | 26 | 27 |
| 6 | 12 | 13 |
| 7 | -- | -- |
+---+----+----+
2 (miss), 3 (hit) 11, 16, 21, 13, 64, 48, 19 (all misses), 11 (hit), 3, 22, 4, 27, 11 (all misses)
Solution
You can try out all of these exercises in the cache simulator below!
Whenever we have to decide to which set a given address belongs to, it is useful to think about the address’ representation in binary notation. If the block contains multiple words, the least significant bits of the address will determine the word index within the block. The following bits will determine the index of the set. The most significant bits are kept as the tag, which does not play a role in this exercise.
For the direct-mapped cache with 16 1-word blocks, we do not have any word index bits, as one block only contains one word. To index 16 bits, we need the least significant log_2(16) = 4 bits of the address. We might notice that these 4 bits of the address always equal to the result of address % 16 , as the more significant bits represent a part of the address that is a multiple of 16.
Taking 42 = 101010 as an example:
6 4 0
+----+------+
| 10 | 1010 |
+----+------+
The lowest 4 bits (the set index) give the result of 42 % 16 = 10 , while the upper bits (the tag) give the result of integer division: 42 // 16 = 2 . Of course, the sum of these is the original address: 2 * 16 + 10 = 42 .
Using this method, we can place all of the addresses in the first exercise, by using the modulo operation to find the correct set. If a given address maps to a block that is already occupied, we simply replace the contained value (and in practice, we would also replace the tag to know which address the value belongs to).
+----+----+
| S | W |
+----+----+
| 0 | 48 |
| 1 | -- |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 21 |
| 6 | 22 |
| 7 | -- |
| 8 | -- |
| 9 | -- |
| 10 | -- |
| 11 | 11 |
| 12 | -- |
| 13 | 13 |
| 14 | -- |
| 15 | -- |
+----+----+
One hit at the second reference to 11.
If one block contains multiple words, we need to pay attention to two things: first, the lowest bits of the address will be used to index the word within the block, not the set.
In the second exercise, we have a block size of 4 bits, so we use the least significant 2 bits of the address to index these.
As the total size is 16 bits, we only have 4 sets. This means that the next two bits of the address will be used to index these sets.
Taking the example of address 42 again, the last two bits are 10 , so within a block, this address will be assigned to the third (watch out, we start from 0!) word. The next two bits in the address are coincidentally also 10 , so we know that it belongs to set 2.
We can again use a trick: we see that the position of the address in the cache is completely determined by the last 4 bits, so the result of the % 16 operation again enough to place it.
The second thing we need to pay attention to is that when a word within a block is loaded, the neighboring values are also updated (cf. spatial locality). In other words, if address 1 is loaded from memory, the values of the memory locations of 0-3 are all loaded into the block in set 1.
+---+----+----+----+----+
| S | W0 | W1 | W2 | W3 |
+---+----+----+----+----+
| 0 | 0 | 1 | 2 | 3 |
| 1 | 4 | 5 | 6 | 7 |
| 2 | 8 | 9 | 10 | 11 |
| 3 | 12 | 13 | 14 | 15 |
+---+----+----+----+----+
2, 3 (H), 11, 16, 21, 13, 64, 48, 19, 11 (H), 3, 22 (H), 4, 27, 11
If our cache has multiple ways, that does not change the addressing. Within one set, the same addresses can be assigned to any of the blocks in each of the ways. If only some of the ways have valid values stored, a new address will be stored in an unoccupied way. If all of the ways are taken, we usually follow a Least Recently Used (LRU) replacement strategy, which means that we replace the block that has been accessed the longest time ago.
In the third exercise, we have a 2-word block size, so the last bit of the address is used for indexing the word. We know that the cache is 2-way set associative, and has a total size of 16 words. With the block size, this gives us 8 blocks, which are divided into 4 sets, as each set contains two blocks (2-way).
4 sets can be indexed with 2 bits, so in total we use 3 bits of the address for indexing, we can take address % 8 to determine which set and word an address belongs to. The choice of block within the set is down to the replacement strategy we use. Once again, we also need to make sure to only replace full blocks, not just one word in the block.
+---+---+----+----+
| S | B | W0 | W1 |
+---+---+----+----+
| 0 | 0 | 48 | 49 |
| | 1 | 64 | 65 |
| 1 | 2 | 26 | 27 |
| | 3 | 10 | 11 |
| 2 | 4 | 4 | 5 |
| | 5 | 12 | 13 |
| 3 | 6 | 22 | 23 |
| | 7 | -- | -- |
+---+---+----+----+
2, 3 (H), 11, 16, 21, 13, 64, 48, 19, 11 (H), 3, 22, 4, 27, 11
Exercise 6
Associativity usually improves the hit ratio, but not always. Consider a direct mapped cache with 16 1-word blocks and a 2-way set-associative cache with 1-word block size and a total size of 16 words. Find a sequence of memory references for which the associative cache experiences more misses than the direct mapped cache.
Solution
The strength of the 1-word block cache is that it has 16 separate blocks. Although the set-associative has just as many blocks, each block has twice as many potential memory addresses mapped on it. If we use a FIFO replacement, a sequence of 8, 16, 0 would insert and remove 8 out of a set-associative cache. The direct mapped cache would still have the 8.
More advanced cache attacks: Prime+Probe
Utilizing knowledge about the cache organization (i.e., placement policies and cache collisions), an attacker can perform cache attacks across protection domains (without shared memory)!
Prime+Probe is a cache attack that allows an attacker to infer information a victim memory accesses without requiring shared memory (unlike Flush+Reload):
- Consider an attacker and a victim executing on the same machine (but without shared memory). The victim has access to a variable
aand the attacker has access to a variablecsuch thataandcmap to the same cache line; - The attacker evicts the address
&afrom the cache by accessing the address&c; - The attacker lets the victim execute. Assuming
secret == 1, the victim requests the address&a, which produces a cache miss; - The address
&ais then requested from DRAM and placed in the cache, evicting the attacker’s datac; - The attacker tries to access again the address
&cand times the memory access. If the access is slow (cache miss) then the attacker can infer thatahas been accessed by the victim, and therefore thatsecret == 1;
OPTIONAL: Exercise 7
Is the above Prime+Probe technique applicable for each of the cache mapping schemes you know: (1) direct mapping, (2) N-way set associative, (3) fully associative with LRU replacement policy? Explain why (not). If applicable, describe a high-level strategy to replace cached victim memory locations by constructing an attacker-controlled eviction set during the “prime” phase. What is the granularity at which an attacker can see victim accesses during the “probe” phase?
Solution
- Direct mapping: Prime+Probe is applicable, since multiple addresses in the main memory map to the exact same cache location. It suffices for the attacker to access a single address with the same cache index address bits in order to replace a cached victim memory address during the “prime” phase. The granularity at which the attacker can later see victim accesses during the “probe” phase, is equal to the cache block size. That is, Prime+Probe cannot distinguish multiple victim accesses within the same cache block.
- N-way set associative: Prime+Probe is applicable, since multiple addresses in the main memory map to the same cache set. However, in order to make sure that a cached victim memory address is replaced during the “prime” phase, the attacker now has to access N addresses with the same cache index address bits (assuming a least-recently used cache replacement policy). The best-case granularity at which the attacker can later see victim accesses during the “probe” phase, is equal to the cache block size. That is, Prime+Probe cannot distinguish multiple victim accesses within the same cache set.
- Fully associative: Prime+Probe is not applicable, since all addresses map to a single set. As such, there is no secret-dependent replacement that can be measured during the “probe” phase. Even if the attacker fully fills the cache during the “prime” phase, she can only learn afterwards that the least-recently used attacker entries were replaced by the victim. In other words, the attacker can only learn how many, but not which victim entries exactly where loaded into the cache.
OPTIONAL: Exercise 8
Consider a processor with a 32-bit addressing mode and a direct mapped cache, with a 1-word block size and a total size of 16 blocks. First calculate index and tag address bits, as in Exercise 4 above. Say that all memory addresses in the range [0, 100[ belong to the victim, whereas the attacker owns addresses in the range[100, 232[. The victim performs a series of address references given as word addresses: either (2, 3, 11, 16, 21, 13, 64, 48, 19, 11, 3, 22, 4, 27, 11) if secret=1, or (2, 3, 11, 16, 21, 13, 64, 48, 19, 11, 70, 36, 7, 91, 75) if secret=0. Construct a memory access sequence to be performed by an attacker during the “prime” phase, in order to learn the victim’s secret in the “probe” phase later on.
Solution
The 32-bit address divided as follows: (26 tag bits), (4 index bits), (2 data bits within word).
Victim’s cache usage (highlighted secret-dependent access sequence for secret=1 vs secret=0):
| S | W |
|---|---|
| 0 |
|
| 1 | – |
| 2 | 2 |
| 3 |
|
| 4 | 4 or 36 |
| 5 | 21 |
| 6 | 22 or 70 |
| 7 | 7 |
| 8 | – |
| 9 | – |
| 10 | – |
| 11 |
|
| 12 | – |
| 13 | 13 |
| 14 | – |
| 15 | – |
Now observe that cache block 7 is only accessed by the victim if secret=0. It thus suffices to load an attacker-controlled memory location that maps to cache block 7 during the “prime” phase (e.g., word address 135), and reload that location in the “probe” phase after the victim’s execution. A long access time (i.e., cache miss) reveals that the attacker’s memory location in cache block 7 was replaced by the victim, and hence secret=0.
OPTIONAL: Exercise 9
Repeat the previous exercise for a processor with a 32-bit addressing mode and a 2-way set-associative cache, with 2-word block size and a total size of 16 words. You can assume a least-recently used cache replacement policy.
Solution
The 32-bit address divided as follows: (27 tag bits), (2 index bits to select set), (1 bit to select word within set), (2 data bits within word).
Victim’s cache usage (highlighted secret-dependent access sequence for secret=1 vs secret=0):
| Set | Block | Word 0 : Word 1 |
|---|---|---|
| 0 | 0 |
|
| 1 | 64:65 | |
| 1 | 2 |
|
| 3 |
| |
| 2 | 4 |
|
| 5 | 12:13 | |
| 3 | 6 | 22:23 or 70:71 |
| 7 | 6:7 |
Now observe that cache set 3 has a higher pressure when secret=0 (two replacements when accessing words 70 and 7) vs. when secret=1 (only a single replacement when accessing word 22). It thus suffices to completely fill cache set 3 with attacker-controlled words (e.g., word addresses 126 and 134) during the “prime” phase. After executing the victim, the attacker reloads both word 126 and 134 in the “probe” phase. Only when both accesses are slow (i.e., cache miss), the victim replaced two cache blocks in cache set 3, and hence secret=0.