Table of contents
Introduction
In the previous sessions, you have seen how to allocate fixed (static) amounts of memory to store program variables or arrays in the .data section. In this session, you will learn how to dynamically allocate memory for data structures that can be resized at runtime (for instance, Python lists or Java ArrayLists).
Recap: pointers in C
In the first exercise session, you had an introduction to pointers in C. We’ll now give a quick reminder about how to use pointers. In this session we will use pointers a lot; if necessary, you can go back to the explanations in the first exercise session or ask your teaching assistant for more explanations.
Variables are stored in memory and have an address. The address of a variable i can be obtained with &i. For instance, if an integer i is stored in the memory at address 0x7f698878, then &i returns 0x7f698878.
A pointer is a variable that stores an address. For instance, a pointer that points to the variable i is declared with int *j = &i, meaning j contains the address of i. A pointer can be dereferenced to access the corresponding data. In C, dereferencing the pointer j is written *j and returns the value at the address pointed by j (here the value of i).
Here is an example of a C program using pointers. Remember that %p is used to print pointers:
| pointers.c | Output |
|---|---|
| |
Using the information that was printed, we can reconstruct the memory layout of the program during the execution:
| Address | Value | Program variable |
|---|---|---|
| … | … | |
| 0x7f698878 | 0x00000005 | i |
| 0x7f69887c | 0x00000005 | k |
| 0x7f698880 | 0x7ffe5f78 | j |
| … | … |
Notice that the order of variables in memory chosen by the compiler is not necessarily the same as the order you declared your variables in the program.
Pointer arithmetic
A pointer is an address, which is a numeric value, therefore one may wonder if it is possible to perform arithmetic operations on pointers. However, if you think about it, it does not really make sense to try to multiply pointers or add two pointers to each other. Thus, only a few arithmetic operations are allowed on pointers:
- Increment/decrement pointers
- Add/subtract integers to pointers
- Subtract two pointers of the same type (we won’t detail this use case but if you’re interested you can have a look at this external resource)
In the following program, we increment a char pointer and an int pointer and print the resulting value:
#include <stdio.h>
int main(void) {
int a = 1;
char *c = "abcd";
int *p = &a;
printf(" c = %p, p = %p\n", c, p);
printf("c + 1 = %p, p + 1 = %p\n", c + 1, p + 1);
}
Suppose the first printf prints c = 0x50000044, p = 0x80000044. What output do you expect for the second printf?
Warm-up 1: Try to run this program on your computer. Does the output match your expectation?
Solution
If the first
printfprintsc = 0x50000044, p = 0x80000044, the secondprintfwill printc + 1 = 0x50000045, p + 1= 0x80000048. The pointer oncharincreases by 1 while the pointer onintincreases by 4.
In C, pointer arithmetic does not follow the same rules as standard integer arithmetic: when a pointer is incremented, its value increases by the size of its corresponding data type. Hence, incrementing a pointer of type char * increases its value by 1 (because the size of a char is 1 byte) whereas incrementing a pointer of type int * or char ** increases its value by 4 (because the size of int or char * is 4 bytes).
More generally, if you have a pointer type *p and an integer n, p += n actually increases the value of the pointer p by n * sizeof(type). The same rule holds when subtracting a pointer with an integer: p -= n decreases the value of the pointer p by n * sizeof(type).
As we will see in the next section, pointer arithmetic is especially convenient for iterating through arrays.
Pointers and arrays
In the second exercise session we have seen how to represent a collection of homogeneous elements using arrays.
For instance, an array of 4 integers can be defined like this:
int a[] = {1, 2, 3, 4};
The value of the array a is the address of the first element of the array: a == &a[0]. It is even possible to use *a = 5 to assign 5 to the first element of the array, just like with a pointer! In that sense, an array is a bit similar to a pointer to the first element of the array.
Contrary to pointers, arrays variables cannot be modified (they are immutable). Hence, you cannot do
a = a + 1.
However, it is possible to define a pointer int *p = a to iterate through the array:
| Example.c | Output |
|---|---|
| |
Exercise 1
Consider the following C function, where in1, in2 and out are all pointers to arrays of n integers. What does the function do? Translate this function to RISC-V.
void sum(int *in1, int *in2, int *out, int n) {
for (int i = 0; i < n; i++) {
*out = *in1 + *in2;
out++;
in1++;
in2++;
}
}
Solution
.globl main
.data
in1: .word 1, 2, 3, 4, 5
in2: .word 5, 4, 3, 2, 1
out: .space 20
n: .word 5
.text
#Takes in1 in a0, in2 in a1, out in a2 and n in a3
sum:
beqz a3, end # Abort if n==0
lw t0, (a0)
lw t1, (a1)
add t0, t0, t1
sw t0, (a2)
addi a0, a0, 4
addi a1, a1, 4
addi a2, a2, 4 # Add 4 to $a 0-3
addi a3, a3, -1 # n--
j sum
end:
ret
main:
la a0, in1
la a1, in2
la a2, out
la t0, n
lw a3, (t0) # Prepare params
jal sum # Call sum
Exercise 2
The following C function compares two strings. It returns 1 if they are equal and 0 if they are not. Notice how we don’t need to pass the length of the strings for this function! Translate this function to RISC-V.
int streq(const char *p1, const char *p2) {
while (*p1 == *p2) {
if (*p1 == '\0') {
return 1;
}
p1++;
p2++;
}
return 0;
}
Solution
.data
a: .string "abcd"
b: .string "abcd"
.globl main
.text
streq:
lb t0, (a0)
lb t1, (a1)
beq t0, t1, loop
li a0, 0 #return 0
ret
loop:
beqz t0, ret1
addi a0, a0, 1
addi a1, a1, 1
j streq
ret1:
li a0, 1 #return 1
ret
main:
la a0, a
la a1, b
jal streq
Dynamic data structures
Arrays in C are static: they must be declared with a fixed length that is known at compile time. This comes with some limitations, for instance if the size is not known at compile time but only determined at runtime, or when the size grows dynamically (the size increases or decreases at runtime).
Dynamic (i.e., resizeable) data structures come by default with many high-level programming languages, such as List in Python or ArrayList in Java, but not in C. Then how can we create the equivalent of a Python List in C?
A possible solution is to reserve a very large static array for every list.
Problem:
- We have to allocate more than we actually need and the extra allocated memory is wasted;
- What if the list grows even bigger?
In the next sections, we will first see how to create dynamic data structures starting with lists, and then generalize to any dynamic data structures.
Linked lists
Assume that a program reserves a big chunk of memory that it can use to store several lists:
.data
list_memory: .space 1000000
Warm-up 2: Can you think of a way to combine multiple fixed size arrays to make a dynamically growing list in
list_memory?
Solution:
A list can be implemented as a set of static arrays chained together using pointers. When one of the arrays is full, just create a new array and chain it with the previous one! This is called a linked list.
Let’s illustrate the concept of linked lists with a running example:
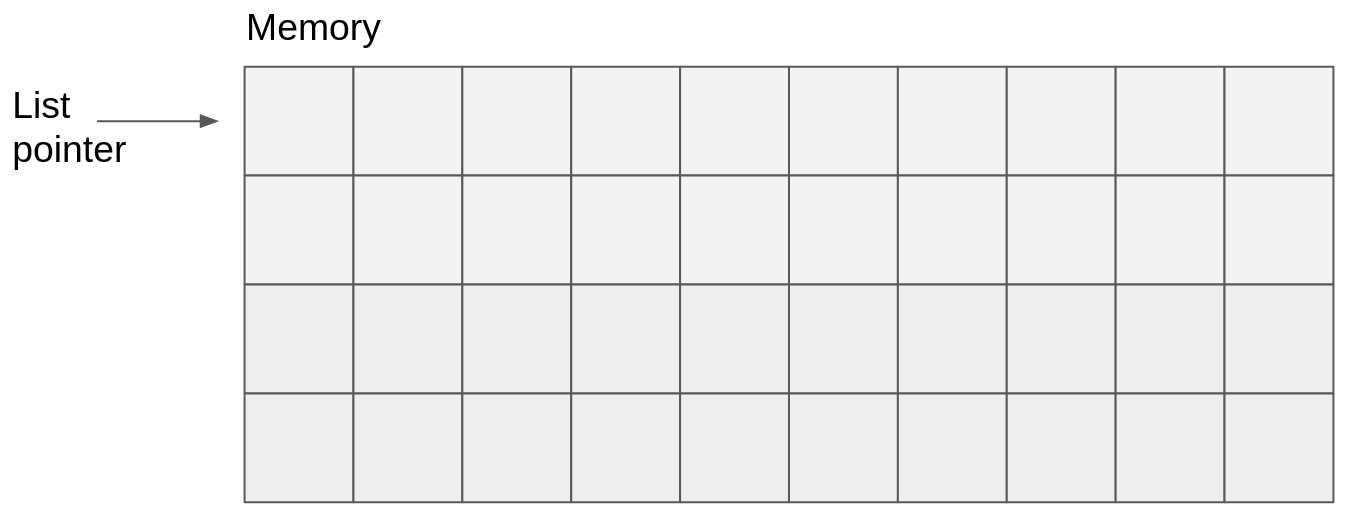
-
Initialization: We use a pointer, called list pointer to record the address of the next free memory location. (This is a bit similar to the stack pointer that you’ve seen in the last session.)
-
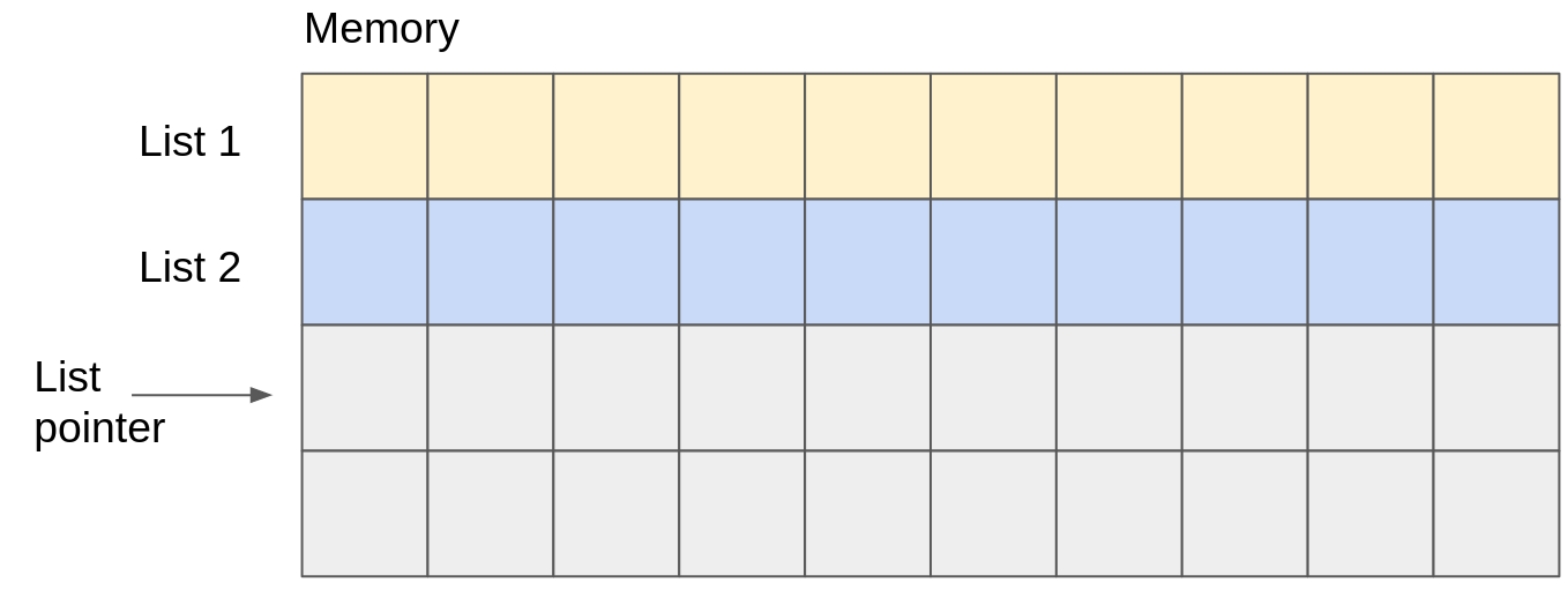
Define a new list: We will use arrays of size 10 as the basic building block to implement our lists. Here we have defined two lists, meaning that we have allocated two consecutive arrays of size 10, and moved the list pointer to point to the next free memory location.
-
Increase size of a list: When
List 1is full, we can extend it by allocating a new array in the free memory. In order to chain both arrays and get a list, we keep a pointer to the second array in the last cell of the first array. In the end, we just need the pointer to the first array ofList 1to reconstruct the whole list!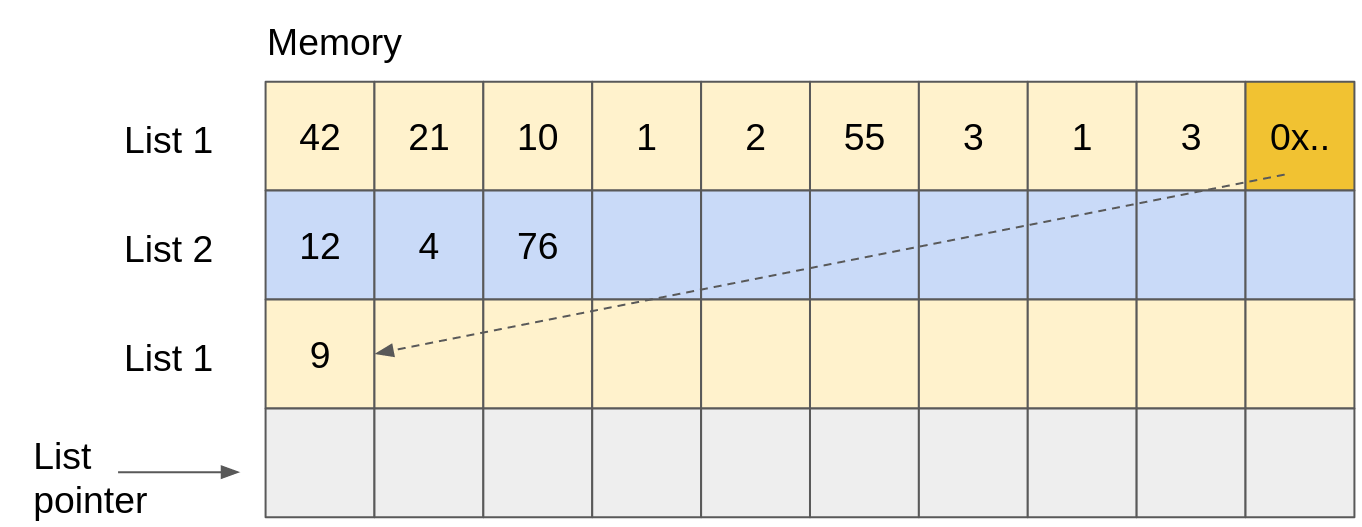
RISC-V implementation
Let us now see how to implement this in RISC-V.
First, we need to store the list pointer in a register. Let us (randomly) pick s9.
la s9, list_memory
Then, to create a list we need to:
- Reserve space for a new array and update the list pointer in
s9to point to the next free memory location. This means increasing the value ofs9by the size of the array (40); - Return a pointer to the newly allocated array (i.e., the old value of
s9).
allocate_list: # Assume s9 keeps track of next free memory location
mv a0, s9 # Return old value of s9 as a pointer to new list
addi s9, s9, 40 # Update the value of list pointer in s9
ret
Notice that the function
allocate_listbreaks the calling conventions because it modifies the callee-saved registers9and does not restore its value. For simplicity, in this session, we will consider thats9is a special register that holds the address for allocating dynamic memory and therefore it should not be modified by any other function than our allocator.
When the list is full, we need to:
- Allocate a new array by calling
allocate_list - Link it to the previous one by storing the address of the newly created array in the last cell of the previous array. Assuming the pointer to the previous list is located in
s0, this can be achieved with the following code:
jal allocate_list # Allocate new array
sw a0, 36(s0) # Link the second part of the list to the first one
Warm-up 3: put all pieces together to reconstruct the illustration with
List 1andList 2given above. You can store the pointer toList 1ins0and the pointer toList 2ins1
Solution
.data
list_memory: .space 1000000
.globl main
.text
allocate_array: # Assume s9 keeps track of next free memory location
mv a0, s9 # Return old value of s9 as a pointer to new list
addi s9, s9, 40 # Update the value of list pointer in s9
ret
main:
# Initialize the list pointer
la s9, list_memory
# Create List 1 and store its address in s0
jal allocate_array
mv s0, a0
# Create List 2 and store its address in s1
jal allocate_array
mv s1, a0
# Fill List 1 with [42, 21, 10, 1, 2, 55, 3, 1, 3]
li t0, 42
sw t0, 0(s0) # s0[0]
# [...]
li t0, 3 # s0[8]
sw t0, 32(s0)
# Fill List 2 with [12, 4, 76]
li t0, 12
sw t0, 0(s1)
# [...]
li t0, 76
sw t0, 8(s1)
# Expand the list
jal allocate_array
sw a0, 36(s0)
# Store last value 9 in List 1
li t0, 9
lw t1, 36(s0) # Load address of second lisk chunk
sw t0, 0(t1) # Store 9 at the beginning of second list chunk
We now have a dedicated memory to store lists and an allocator to make our lists grow (almost) as large as we want! However, our solution only allows lists, while there are many more useful data structures. Let’s see how we can extend our solution to work with other data structures.
Generalize to all data structures: the heap
In the RISC-V memory layout, illustrated below, the .data section is used to store statically allocated data (such as C arrays or constants) while the heap segment holds dynamically allocated data structures like lists, trees, etc.
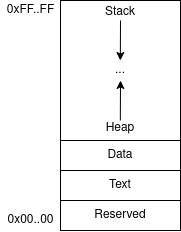
In the next session, you will see how to actually ask the operating to dynamically allocate memory for your program. For now, we will adopt a simpler approach and consider that we have a dedicated space for the heap in the .data section:
.data
heap: .space 1000000
What we want is to use that heap to allocate arbitrary data structures. For instance, in the following example: we first allocate a list, then a binary tree, and finally extend the first list (click or slide through the images).
To be able to allocate memory for different data structures, we need to generalize the allocator that we defined before (allocate_list) to allocate arbitrary large chunks. This is simple, we can just add the size as a parameter to the function:
allocate_space: # Assume that s9 keeps track of the next free memory location in the heap
mv t0, a0 # The size to allocate is provided as an argument to the function
mv a0, s9 # Return old value of s9 as a pointer to the new allocated space
add s9, s9, t0 # Update the value of heap pointer in s9
ret
Finally, we can re-implement our simple list allocator using our new allocate_space:
allocate_list:
addi sp, sp, -4
sw ra, (sp)
li a0, 40
jal allocate_space
lw ra, (sp)
addi sp, sp, 4
ret
main:
la s9, heap
jal allocate_list
Exercise 3
Create a dynamic stack data structure on the heap (see the illustration below for an example). Complete the gaps (cf. #TODO) in the RISC-V program below. Use the simple allocator allocate_space and write the following missing functions in RISC-V (consider that stack_pointer is the type of the pointer to the top pointer):
-
stack_pointer stack_create(void): Creates a new, empty stack: it allocates space for thetoppointer.- Allocates enough heap memory to store the
toppointer. - Since the stack is empty, initialize this
toppointer to0: (this is called a null pointer). - Return the address of this
toppointer ina0. This can be considered the address of the stack (inmainyou should keep this pointer in a safe place, it is the pointer that you will use to reconstruct the whole stack!).
- Allocates enough heap memory to store the
-
void stack_push(stack_pointer, int): Adds a new element on the stack.- The function takes the address of the
toppointer ina0and the value to be pushed on the stack ina1. - It allocates enough heap memory to store the new value and to store a reference to the previous top element.
- It initializes the newly allocated element (first word to value, second word to address of previous top element).
- It updates the
toppointer to point to the newly allocated element.
- The function takes the address of the
-
int stack_pop(stack_pointer): Removes and returns the top element from a stack.- The function takes the
toppointer ina0. - It updates the
toppointer to point to the element before the current top element. - Finally, it return the value of the popped element in
a0. Don’t forget the calling conventions!
- The function takes the
.globl main
.data
heap: .space 1000000
.text
allocate_space:
mv t0, a0
mv a0, s9
add s9, s9, t0
ret
stack_create: #TODO
stack_push: #TODO
stack_pop: #TODO
main:
la s9, heap
# Test code
jal stack_create # Create stack -> top pointer in a0
addi sp, sp, -4
sw a0, (sp) # Push top pointer on call stack
# Push 1 to stack
li a1, 1
jal stack_push
# Push 2 to stack
lw a0, (sp)
li a1, 2
jal stack_push
# Push 3 to stack
lw a0, (sp)
li a1, 3
jal stack_push
# Verify the state of the stack using the single step function!
# It should look like the picture below.
# Pop 3 from stack
lw a0, (sp)
jal stack_pop
# Pop 2 from stack
lw a0, (sp)
jal stack_pop
# Verify that a0 equals 2 now
# Verify that the stack top now points to the value 1
addi sp, sp, 4

Solution
.globl main
.data
heap: .space 1000000
.text
allocate_space:
mv t0, a0
mv a0, s9
add s9, s9, t0
ret
stack_create:
addi sp, sp, -4
sw ra, (sp)
li a0, 4
jal allocate_space
sw zero, (a0) #Don't assume allocated memory is zero
#For this simple allocator this is the case,
#but more complex allocators might break this assumption
lw ra, (sp)
addi sp, sp, 4
ret
#Stack push should replace top (in a0) with a new address
#The new element should point to the old top
stack_push:
addi sp, sp, -12
sw ra, (sp)
sw a0, 4(sp) #Back up the top address on the stack
sw a1, 8(sp) #Back up the value-to-push
li a0, 8 #Allocate space for 2 words
jal allocate_space #New node address in a0
lw t0, 4(sp) #Address of top poiner in t0
#Modify top
lw t1, (t0) #Load old top address in t1
sw a0, (t0) #Store new node address as new top value
#Init node
sw t1, 4(a0) #Store old top address in new node pointer
lw t1, 8(sp) #Load value-to-push in t1
sw t1, (a0) #Store value-to-push in new node
lw ra, (sp)
addi sp, sp, 12
ret
stack_pop:
lw t0, (a0) #t0 = address of first node on stack
lw t1, 4(t0) #t1 = address of second node on stack
sw t1, (a0) #Adjust top pointer to point to second stack node
lw a0, (t0) #a0 = value of first node on stack
ret
main:
la s9, heap
#Test code
jal stack_create #Create stack -> top pointer in a0
addi sp, sp, -4
sw a0, (sp) #Push top pointer on call stack
#Push 1 to stack
li a1, 1
jal stack_push
#Push 2 to stack
lw a0, (sp)
li a1, 2
jal stack_push
#Push 3 to stack
lw a0, (sp)
li a1, 3
jal stack_push
#Verify the state of the stack using the single step function!
#At this point, the top pointer should point to the value 3.
#The next word in memory is a pointer to the value 2.
#At that location, 2 is stored.
#The next word in memory is then a pointer to the value 1.
#The next word in memory after value 1 should be the value 0.
#Pop 3 from stack
lw a0, (sp)
jal stack_pop
#Pop 2 from stack
lw a0, (sp)
jal stack_pop
#Verify that a0 equals 2 now
#Verify that the stack top now points to the value 1
addi sp, sp, 4
Exercise 4
Would it be possible to allocate growing data structures, like a binary tree or a linked list, on the call stack? The following code provides a suggestion for a simple allocator that tries to do exactly this. Can you see any problems with this approach?
allocate_stack:
mv t0, a0
mv a0, sp
sub sp, sp, t0
ret
Solution:
Allocating dynamic memory on the stack is not possible:
- The
spregister is callee-save, so theallocate_stackfunction breaks the calling conventions. - That also means that when you call
allocate_stack, your function will break the calling conventions if it doesn’t restore the stack pointer. - If you do restore the stack pointer, you are also deallocating dynamic memory that has been reserved in this function. In theory, yes, you can allocate on the stack. But then the allocated dynamic memory can never live longer than the function itself, since you need to restore the stack pointer (deallocate the memory) before returning. That makes a simple function such as the
stack_createorstack_pushfrom previous exercises impossible to write. They simply can’t return addresses to newly allocated stack space - it has to be deallocated first!
Exercise 5
Can you come up with an allocator function that allows you to free previously allocated memory? The allocator should reuse previously freed memory. The following steps might help:
- Store the address of the first empty (free) heap region in a global variable,
- Allocate space for metadata when creating chunks,
- Store the size of a chunk in the chunk metadata,
- For free chunks, also store the address of the next free chunk in the chunk metadata.
Solution
.data
next_free: .word 0
heap: .space 1000000
.globl main
.text
#a0: amount of words to allocate
#Allocation format:
# 4 bytes | 4 bytes | a0 words
# First 4 bytes store either 0 (if the chunk is allocated) or the address of the next free chunk
# (if the chunk is not allocated, thus part of a free list)
# Second 4 bytes store the size in bytes of the third region
# The third region is a0 words in size and contains the actually reserved memory
allocate:
#First, we will go through the free chain to see if any previously freed chunk is big enough for our allocation
#We will take the strategy that any chunk that fits is good enough
#There are many different strategies to take here, each have advantages and disadvantages
li t0, 4
mul a0, a0, t0 #Convert words to bytes
#The following loop will search through the free chunks until it finds one that fits the requested allocation size
#If none fit, a new chunk is allocated
lw t0, next_free
la t3, next_free
j skip
chunk_loop:
mv t3, t2
skip:
beqz t0, new_chunk #If there is no free chunk, allocate a new one
lw t1, 4(t0) #If there is a free chunk, get the size of that chunk in t1
mv t2, t0 #Copy the free chunk address (in case we will use the chunk)
lw t0, 0(t0) #Load the address of the next free chunk in t0 (in case current chunk is too small)
blt t1, a0, chunk_loop #Not enough space in the free chunk, find the next one by looping
#If you get in this part of the code you have found a big enough chunk in the free list
#The address of this chunk is in t2
#Re-use this chunk by removing it from the free list
#Make sure to restore the free list properly
#t3 should now have the location where we need to store the address of the next chunk
#t0 contains the address of the next chunk
sw t0, (t3)
#Return the actual chunk addr
mv a0, t2
#Don't point to the metadata
addi a0, a0, 8
ret
new_chunk:
sw zero, (s9) #Store 0 in the first 4 bytes to denote the fact this chunk is allocated
sw a0, 4(s9) #Store the chunk size in the next 4 bytes
addi s9, s9, 8 #Move the s9 by 8 - the actual start of the newly reserved memory
mv t0, a0 #Back-up the bytes to reserve in t0
mv a0, s9 #Return the actual start of the newly reserved memory
add s9, s9, t0 #Reserve bytes by incrementing the s9
ret
#Address of chunk to free in a0
#next_free always points to the chunk metadata, not the chunk data (chunk data addr = chunk metadata addr + 8)
free:
lw t0, next_free #Address of the next free chunk in t0
addi a0, a0, -8 #Move to chunk metadata
sw t0, (a0) #Store address of next free chunk in this free chunk
sw a0, next_free, t0 #Update next free to point to the newly freed chunk
ret
main:
la s9, heap
li a0, 1 #Allocate 4 bytes
jal allocate
li t0, 123
sw t0, (a0) #Store 123 in newly allocated region
jal free #Free allocated 4 bytes
li a0, 2
jal allocate #Allocate 8 bytes
li t0, 234
sw t0, (a0) #Store 234 in newly allocated region
jal free #Free allocated 8 bytes
li a0, 1
jal allocate #Allocate 4 bytes - should re-use 8 byte region that was just freed
li t0, 345
sw t0, (a0) #Store 345 in the 8-byte region (even though 4 bytes were asked, we used a bigger chunk)
li a0, 1 #allocate 4 bytes
jal allocate #Re-use first 4 bytes
li t0, 456
sw t0, (a0)